FPB dan Aplikasinya

Bahasan mengenai Faktor Persekutuan Terbesar beserta aplikasinya dalam soal cerita.

Halo Sahabat Gurnulis. Berjumpa lagi dengan penulis ya. Penulis kali ini masih tetap mengetengahkan artikel mengenai materi pembelajaran. Penulis hendak membahas FPB atau Faktor Persekutuan Terbesar. Tentunya bahasan ini tidak asing bagi kita. Yuk, sama-sama kita bahas.

Pengertian FPB

FPB atau Faktor Persekutuan terBesar adalah bilangan bulat positif terbesar yang dapat membagi habis bilangan-bilangan tertentu. Istilah FPB tersedia dalam beberapa bahasa. Dalam bahasa Inggris FPB dikenal dengan istilah-istilah berikut.

Greatest Common Divisor (GCD),
Greatest Common Factor (GCF), atau
Highest Common Factor (HCF).

Manfaat FPB

Untuk apa kita belajar FPB? FPB bermanfaat dalam mencari nilai pecahan yang paling sederhana. Misalnya, pecahan paling sederhana dari ⁹⁰/₁₂₀ adalah ³/₄ karena FPB dari 90 dan 120 adalah 30, maka disederhanakan menjadi ⁹⁰/₁₂₀ = ^90:30/_120:30 = ³/₄.

Selain itu, dalam kehidupan sehari-hari, ada kalanya kita dihadapkan pada suatu permasalahan yang dapat diselesaikan dengan mengetahui FPB-nya. Contohnya dalam kasus berikut.

Ibu mempunyai 24 buah salak dan 30 buah jeruk. Salak dan jeruk tersebut akan dihidangkan dalam pertemuan di rumah. Ibu ingin membagikan buah-buahan tersebut ke dalam beberapa tempat buah dengan isi buah jeruk dan salak yang sama banyak. Berapa banyak model susunan buah dalam tempat buah? Berapa banyak salak dan jeruk pada masing-masing model? Berapa tempat buah terbanyak yang diperlukan ibu?

Cara Mencari FPB Menggunakan Tabel

Pada dasarnya kasus yang melibatkan FPB itu memiliki ciri khas, yaitu terdapat kata “paling banyak” atau “terbanyak” atau “maksimal” pada pertanyaannya. Terkadang masih kita jumpai pertanyaan yang salah (tanpa kata tersebut) namun jawaban penyelesaiannya menggunakan FPB.

Kita kembali pada kasus di atas.

Ibu mempunyai 24 buah salak dan 30 buah jeruk. Salak dan jeruk tersebut akan dihidangkan dalam pertemuan di rumah. Ibu ingin membagikan buah-buahan tersebut ke dalam beberapa tempat buah dengan isi buah jeruk dan salak yang sama banyak. Berapa banyak model susunan buah dalam tempat buah? Berapa banyak salak dan jeruk pada masing-masing model? Berapa tempat buah terbanyak yang diperlukan ibu?

Permasalahan di atas dapat diselesaikan dengan memberi tanda langsung pada tabel angka seperti berikut. Tabel angka biasanya digunakan untuk persoalan sederhana yang bilangannya tidak besar. Untuk permasalahan di atas kita gunakan tabel angka sampai 50.

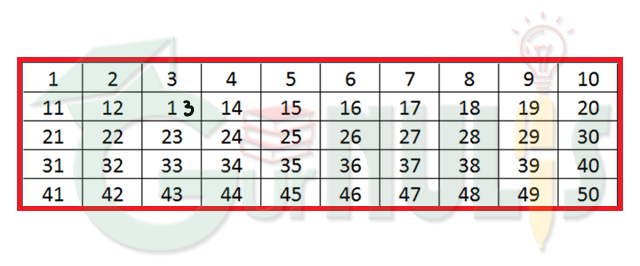
Langkah-langkah yang ditempuh adalah sebagai berikut.

Tentukan faktor dari 24 dan 30. Faktor dari 24 adalah 1 ,2, 3, 4 ,6, 12, dan 24. Faktor dari 30 adalah 1, 2, 3, 5, 6, 10, 15, dan 30.
Beri tanda yang berbeda faktor-faktor tersebut pada tabel angka. Untuk faktor-faktor 24 lingkari angkanya dengan warna biru dan faktor-faktor 30 dengan stabilo kuning. Perhatikan gambar berikut!
Perhatikan angka yang mempunyai 2 simbol sekaligus. Tampak dari tabel di atas, faktor persekutuan dari 24 dan 30 adalah 2, 3, dan 6.
FPB dari bilangan tersebut adalah faktor terbesar dari faktor persekutuannya. Jadi FPB dari 24 dan 30 adalah 6.

Cara Mencari FPB Menggunakan Pohon Faktor

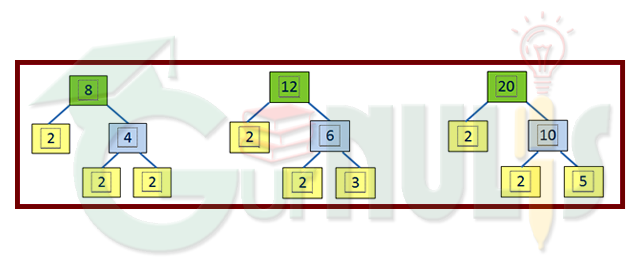
Kita ambil contoh mencari FPB dari 8, 12, dan 32. Ketiga bilangan tersebut dapat dicari FPB-nya menggunakan pohon faktor sebagai berikut.

Pohon faktor untuk membuat faktorisasi prima dari 8, 12, dan 20.
8 dibagi 2 hasilnya adalah 4 dan 4 dibagi 2 hasilnya adalah 2;
12 dibagi 2 hasilnya adalah 6 dan 6 dibagi 2 hasilnya adalah 3;
20 dibagi 2 hasilnya adalah 10 dan 10 dibagi 2 hasilnya adalah 5.
Faktorisasi primanya adalah sebagai berikut.
8 = 2 ×2 × 2 = 2³
12 = 2 × 2 × 3 = 2² × 3
20 = 2 × 2 × 5 = 2² × 5
Memilih faktor prima yang berpangkat paling kecil, hingga didapatkan 2².
FPB dari 8, 12, dan 20 adalah 2²= 4.

Contoh Penyelesaian Soal Cerita dengan FPB

Perhatikan soal cerita berikut!

Pak Amir mempunyai 20 roti goreng dan 30 tahu bakso. Makanan tersebut akan dimasukkan kedalam kotak snack dengan jumlah yang sama banyak.
a. Berapa kotak yang diperlukan untuk membungkus makanan tersebut?
b. Berapa banyak roti goreng dan tahu bakso pada masing-masing kotak?

Penyelesaian dari soal tersebut adalah sebagai berikut.

Faktorisasi prima dari 20 = 2 × 5

Faktorisasi prima dari 30 = 2 × 3 × 5

FPB dari 20 dan 30 = 2 × 5 = 10

a. Banyak kotak yang diperlukan adalah 10

b. Banyak roti goreng dalam setiap kotak = 20 : 10 = 2 dan banyak tahu bakso dalam setiap kotak = 30 : 10 = 3.

Sekarang kita cermati kembali pertanyaan pada butir "a" di atas. Sebenarnya pertanyaan tersebut benar. Namun jika kita melihat jawabannya, berarti pembuat soal tersebut bermaksud menyusun soal FPB. Apa yang kurang dari pertanyaan tersebut jika kita ingin menyempurnakannya? Masih ingatkah rambu-rambu dalam menuliskan soal FPB di atas?

Pertanyaan FPB biasanya ada kata “terbanyak”, “paling banyak”, atau “maksimal”. Jadi seharusnya pertanyaan tersebut menjadi: Berapa kotak paling banyak yang diperlukan untuk membungkus makanan tersebut?

Pertanyaan "a" di atas bersifat terbuka, jawabannya bisa lebih dari 1 jawaban. Soal tersebut berkaitan dengan faktor persekutuan dari 20 dan 30, bukan FPB. Faktor persekutuan dari 20 dan 30 adalah 1, 2, 5, dan 10.

Jadi banyak kotak yang diperlukan bisa 1, 2, 5, atau 10. Semua kemungkinan jawaban ini menunjukkan isi kotak sama banyak roti goreng dan tahu bakso. Sehingga untuk menjawab banyak roti goreng dan tahu bakso pada masing-masing kotak dapat kita buat dalam tabel berikut.

Tampak bahwa 10 kotak adalah kotak terbanyak yang diperlukan pak Amin, yang ditunjukkan oleh FPB dari 20 dan 30 adalah 10.

Sekarang mari kita coba selesaikan permasalahan berikut.

Pada ulang tahunnya yang ke-10, Falah berencana akan mengundang beberapa anak yatim dan memberi hadiah kepada mereka. Dari uang tabungannya, ia bisa membeli 60 pensil, 90 pulpen, dan 120 buku. Jika Falah ingin memberikan pensil, pulpen, dan buku yang sama banyak untuk tiap anak yatim, maka berapa anak yatim paling banyak yang bisa diundang Falah? Berapa banyak pensil, pulpen, dan buku yang diterima setiap anak yatim tersebut?

Permasalahan di atas berkaitan dengan nilai bilangan yang cukup besar, jadi kita akan selesaikan menggunakan faktorisasi prima sebagai berikut.

Menentukan pohon faktor untuk membuat faktorisasi prima dari 60, 90, dan 120.
gambar
Faktorisasi   primanya adalah:
60 = 2 × 2 × 3 × 5 = 2² × 3 × 5
90 = 2 × 3 × 3 × 5 = 2 × 3² × 5
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3 × 5
Pilihlah faktor prima yang berpangkat lebih kecil dari faktor yang sama. FPB dari 60, 90, dan 120 adalah 2 × 3 × 5 = 30. Jadi anak yatim terbanyak yang bisa diundang Falah adalah 30 anak. Masing-masing anak yatim menerima sebagai berikut.
gambar.

Demikianlah bahasan mengenai FPB dan aplikasi. Semoga informatif ya, Sahabat Gurnulis.

Salam literasi guru ndeso.