Gali-Tempat, Cara Mudah Mengubah Pecahan Biasa ke Desimal

Menalarkan pengubahan pecahan biasa menjadi desimal menggunakan cara Gali-Tempat

Assalamualaikum. Halo sahabat gurnulis, masih menunggu-nunggu artikel baru dari Gurnuliskah? Kalau iya, inilah saat-saat yang tepat untuk membuka blog Gurnulis, karena penulis hari ini menyajikan bahasan yang pastinya menarik! Oh ya, kalau belum sempat membaca tentang cara mudah menalarkan pembagian bersusun (porogapit) kepada peserta didik, sahabat pendidik boleh membacanya terlebih dahulu, ya. Di situ penulis telah berbagai cara menalarkan porogapit melalui garis kelipatan.
 

Pada postingan kali ini penulis ingin berbagi cara mudah untuk menalarkan salah satu operasi hitung pada Matematika. Penulis masih berfokus kepada Matematika mengingat mata pelajaran ini cukup susah untuk dipahami oleh sebagian besar peserta didik dan penalarannya memerlukan bentuk konkret.
 

Salah satu kompetensi Matematika yang memerlukan penalaran konkret dalam operasinya adalah pengubahan bentuk pecahan biasa menjadi desimal. Pecahan biasa, sebagaimana yang kita ketahui, merupakan pecahan yang ditandai dengan tanda per. Angka yang terletak di atas tanda per disepakati sebagai pembilang dan angka yang terletak di bawah tanda per disepakati sebagai penyebut. Desimal sendiri merupakan bentuk pecahan yang dinyatakan dalam digit-digit nilai tempat. Digit pecahan pada bentuk desimal diletakkan setelah tanda koma, ada yang menempati persepuluhan, perseratusan, perseribuan, dan sebagainya.

 

Pengubahan pecahan biasa menjadi desimal dapat ditempuh dalam dua cara. Cara yang pertama adalah dengan membaginya secara langsung dengan pembagian bersusun dan cara yang kedua adalah dengan mengubahnya ke bentuk persepuluhan, perseratusan, perseribuan, dan seterusnya terlebih dahulu, kemudian baru diubah ke bentuk desimal. Pada bahasan ini, penulis menyoroti cara yang kedua.
 

Kita langsung saja menuju ke permasalahan. Contohnya, kita akan mengubah pecahan ⁷⁵⁄₁₀₀ menjadi bentuk desimal. Di sini penulis langsung memberi contoh pecahan berpenyebut 10, 100, 1.000, dan seterusnya, ya. Penulis tidak menyoroti upaya pengubahan dari pecahan selain per 10, 100, 1.000, dan seterusnya hingga menjadi per 10, 100, 1.000, dan seterusnya. Pengubahan pecahan tersebut akan penulis bahas di artikel selanjutnya.
 

Pada buku-buku cetak Matematika jalan pengubahannya diterangkan dengan bahasa "GESER" sebagai berikut.

Pembilang yang diberi tanda desimal sesuai dengan banyak angka 0 pada penyebut. Jika hanya ada 1 angka 0 di penyebut, GESER tanda desimal ke kiri sejauh 1 angka, dan seterusnya.  Karena terdapat 2 angka 0 pada langkah 2, maka tanda desimal DIGESER ke kiri sejauh 2 angka. 

 

Dituliskan angka 0 sebelum tanda koma, sehingga didapatkan bilangan desimal 0,75.

Penjelasan-penjelasan tersebut tentunya memerlukan tutorial dari pendidik. Setelah ditutorkan pun ternyata seringkali memunculkan permasalahan baru. Permasalah yang dimaksud adalah bingungnya peserta didik dalam MENGGESER dan menempatkan angka 0 (nol).
 

Contohnya begini, ketika dihadapkan dengan soal lain, pecahan ⁷⁄₁₀₀ misalnya, bisa jadi penalaran peserta didik akan berubah menjadi sebagai berikut.

⁷⁄₁₀₀ = 0,7 karena asumsinya hanya diperbolehkan ada satu angka nol saja yaitu di depan tanda koma.

Atau juga seperti ini.

⁷⁄₁₀₀ = 0,007 karena asumsinya angka 100 nolnya ada dua, jadi angka tujuhnya digeser dan ditengah-tengahnya diberi dua buah angka nol. Dua buah angka nol ini dipadang sebagai dua kali pergeseran.

Bagaimana dengan soal-soal lain, ⁷⁄_10.000 misalnya? Tentunya kebingungan yang sama akan kembali terjadi.

Analisis Kebingungan Peserta Didik

Sahabat pendidik, yuk sama-sama kita cermati letak kebingungan peserta didik. Pecahanan ⁷⁄₁₀₀ yang dianggap sama dengan 0,7 terjadi karena kesalahan peserta didik dalam menempatkan tanda koma dan angka nol. Peserta didik menganggap kalau angka nolnya cukup dan harus satu saja, yaitu di depan tanda koma. Di sini terlihat peserta didik belum memahami arti dari nilai tempat pada bentuk desimal. Pada pecahan ⁷⁄₁₀₀, yang angka tujuhnya berada pada nilai tempat perseratusan, pada bentuk desimalnya diletakkan pada persepuluhan.
 

Serupa dengan kesalahan sebelumnya, pecahan ⁷⁄₁₀₀ yang dianggap sama dengan 0,007 terjadi karena kesalahan peserta didik dalam menempatkan tanda koma dan angka nol. Pada kasus ini, peserta didik salah dalam "menggeser". Di sini pun terlihat kalau peserta didik belum sepenuhnya memahamai arti dari nilai tempat pada bentuk desimal. Pada pecahan ⁷⁄₁₀₀, yang angka tujuhnya berada pada nilai perseratusan, pada bentuk desimalnya diletakkan  pada perseribuan.
 

Kebutuhan Peserta Didik

Upaya pengubahan pecahan biasa yang telah berpenyebut 10, 100, 1.000, dan seterusnya ke bentuk desimal memerlukan pemahaman yang benar mengenai nilai tempat. Jika pada pecahan biasa tertulis per 10, maka pada bentuk desimalnya pun harus sampai pada nilai persepuluhan. Jika pada pecahan biasa tertulis per 100, maka bentuk desimalnya pun harus sampai pada nilai perseratusan, dan seterusnya.
 

Pada pembelajaran, upaya untuk memahamkan nilai tempat ini memerlukan cara-cara konkret yang mudah dipahami oleh peserta didik. Pendekatan pembelajaran dengan konsep GESER sebagaimana yang sudah terpapar di atas sebenarnya sudah konkret, namun belum cukup mudah dinalar oleh peserta didik. Peserta didik memerlukan cara konkret yang lebih mudah untuk dipahami.

Cara Gali-Tempat untuk Mengubah Pencahan Biasa menjadi Desimal

Adakah cara yang mudah dipahami peserta didik untuk mengubah pecahan biasa menjadi desimal? Ada! Penulis menyebutnya dengan nama "Gali-Tempat".
 

Gali-tempat  merupakan akronim yang mudah diingat dari "Garis Nilai Tempat". Untuk menggunakan cara ini, cukup siapkan pensil dan penghapus.

 

Cara menggunakannya penulis terangkan sebagai berikut. Mohon disimak baik-baik.
 

Kita ambil contoh mengubah pecahan ⁷⁄₁₀ menjadi bentuk desimal.

 

Perhatikan penyebut pecahannya dan fokuskan pada banyaknya angka nol. Penyebutnya adalah 10 dan banyaknya angka nol adalah satu.

 

Karena banyaknya angka nol adalah satu, maka pada sisi desimal dibuat Gali-Tempat (Garis Nilai Tempat) yang berjumlah satu juga setelah tanda koma.

 

Pindahkan pembilang pada garis yang telah dibuat tadi. 

Isi bagian yang kosong dengan angka nol, termasuk ke bagian sebelum tanda koma.

 

Hapus Gali-Tempat dengan menggunakan penghapus.

 

Taraaang... Pengubahan pecahannya terasa mudah, bukan? Pecahan ⁷⁄₁₀ adalah sama dengan 0,7.

Oke, sekarang kita mencoba dengan pecahan yang lain.
Kita ambil contoh mengubah pecahan ⁷⁄₁₀₀ menjadi bentuk desimal.

 

Perhatikan penyebut pecahannya dan fokuskan pada banyaknya angka nol. Penyebutnya adalah 100 dan banyaknya angka nol adalah dua.

 

Karena banyaknya angka nol adalah dua, maka pada sisi desimal dibuat Gali-Tempat yang berjumlah dua juga setelah tanda koma.

 

Pindahkan pembilang pada Gali-Tempat yang telah dibuat tadi. Pemindahan harus dimulai dari BELAKANG.

 

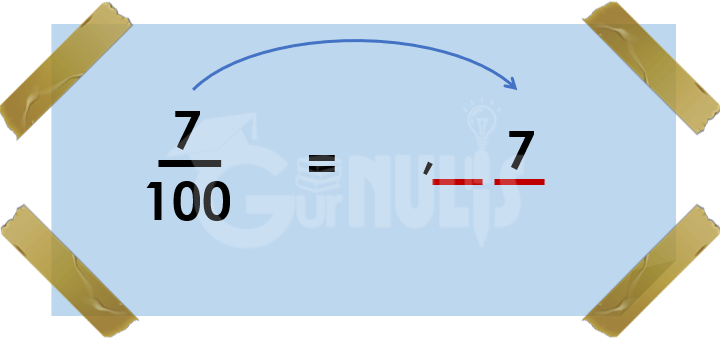
Isi bagian yang kosong pada Gali-Tempat dengan angka nol, termasuk ke bagian sebelum tanda koma.

 

Hapus Gali-Tempat dengan menggunakan penghapus.

Lagi-lagi pengubahan pecahannya terasa mudah, bukan? Didapatkan ⁷⁄₁₀₀ = 0,07.

Bagaimana dengan pembilang yang digit angkanya lebih dari satu? Penulis berikan contoh pengubahannya.
 

Kita ambil contoh mengubah pecahan ¹⁰⁴⁄_10.000 menjadi bentuk desimal.

 

Seperti pada cara sebelumnya, fokuskan perhatian pada penyebut dan banyaknya angka nol. Penyebutnya adalah 10.000 dan banyaknya angka nol adalah empat.

 

Karena banyaknya angka nol adalah empat, maka pada sisi desimal dibuat Gali-Tempat yang berjumlah empat juga setelah tanda koma.

 

Pindahkan pembilang pada Gali-Tempat yang telah dibuat tadi. Pemindahan harus dimulai dari BELAKANG. Pembilang 104, dipindahkan dari angka 4 terlebih dahulu, baru kemudian angka 0, dan angka 1-nya.

 

Isi bagian yang kosong pada Gali-Tempat dengan angka nol, termasuk bagian sebelum tanda koma.

 

Hapus Gali-Tempat dengan menggunakan penghapus.

Taraaang... Sangat mudah bukan mengubah ¹⁰⁴⁄_10.000 menjadi bentuk desimal? Jangan lupa, hasilnya yang berupa 0,0104 itu PASTI BENAR!

Bagaimana dengan bentuk pecahan campuran? Ayo simak lagi penjelasan penulis berikut.
Kita ambil contoh mengubah pecahan ^1.702⁄₁₀₀ menjadi bentuk desimal.

 

Lagi-lagi, fokuskan perhatian pada penyebut dan banyaknya angka nol. Penyebutnya adalah 100 dan banyaknya angka nol adalah dua.

 

Karena banyaknya angka nol adalah dua, maka pada sisi desimal dibuat Gali-Tempat yang berjumlah dua juga setelah tanda koma.

 

Pindahkan pembilang pada Gali-Tempat yang telah dibuat tadi. Pemindahan harus dimulai dari BELAKANG. Pembilang 1.702 dipindahkan dari angka 2 terlebih dahulu, baru kemudian angka 0. Sampai di sini, pemindahan terhalang oleh tanda koma.

 

Pemindahan dilanjutkan pada bagian sebelum tanda koma. Sama dengan cara sebelumnya, pemindahan dimulai dari BELAKANG, dimulai dari angka 7 terlebih dahulu baru kemudian angka 1.

 

Perhatikan kalau di sini tidak ada bagian yang kosong, jadi angka nol tidak perlu diisikan sebagai pemenuh posisi Gali-Tempat yang kosong!

 

Hapus Gali-Tempat dengan menggunakan penghapus.

 

Taraaang... Sangat mudah bukan mengubah ^1.702⁄₁₀₀ menjadi bentuk desimal? Hasilnya adalah 17,02 dan itu PASTI BENAR! Bayangkan, bagaimana senangnya peserta didik kita jika  mengubah pecahannya semudah ini!

Kesimpulan

Cara Gali-Tempat sebenarnya adalah cara mengonkretkan pengubahan pecahan biasa menjadi desimal dengan memperhatikan nilai tempatnya. Kebanyakan peserta didik merasa bingung dengan penjelasan nilai tempat yang ditempuh secara abstrak. Garis-garis yang dibuat pada Gali-Tempat dirasa cukup efektif dalam memahamkannya.

Cara GESER yang dipaparkan oleh buku-buku cetak Matematika seringkali menimbulkan kebingungan peserta didik. Penggunaan cara Gali-Tempat dirasa dapat menjawab kebingungan tersebut. Bagaimana sahabat pendidik, terinspirasikah dengan cara Gali-Tempat ini? Ayo tuliskan pada kolom komentar di bawah ini.

Salam literasi guru ndeso!

Munasifatut Thoifah

Guru yang selalu ingin berbagi inspirasi.

Bagikan Artikel ini